Introduction
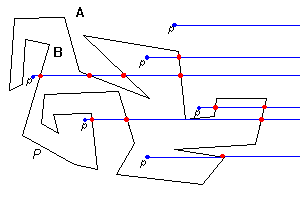
The human eye, after staring for a few seconds at a picture like in Fig. 1, can distinguish the two above mentioned sets A and B. One question that raises is, can a computer determine the two sets A and B in a reasonable amount of time and using a reasonable amount of resources. The answer is yes. Algorithms for point location have been developed and they are quite efficient. The object of this page is to demonstrate a theorem encapsulating some of the properties mentioned above and to show an implementation of a point-in-polygon-testing algorithm, namely, the plumb-line algorithm.
About The Jordan Curve Theorem
|
Any simple closed curve C divides the points
of the plane not on C into two distinct domains (with no points in common)
of which C is the common boundary.[1]
We shall take the case where C is a closed polygon P. |
|
The theorem was first stated by Camille Jordan
(1838 -1922) in his Cours d'Analyse. Proving this theorem
has not been an easy task. The proof given by Jordan himself was quite
complicated and it turned out to be invalid. The difficulty in proving
this theorem lies in the generality of the concept of "simple closed
curve"[1], which is not restricted to the class
of polygons or "smooth" curves, but includes all curves which
are topological images of a circle. Also, concepts like inside and
outside, even though they are intuitively clear, must be defined
precisely before a rigorous proof is possible[1].
|
| As important as it is to thoroughly analyze these concepts before attempting
to prove this theorem, we should also remember to keep this analysis as
simple as possible in order to avoid some difficulties that could arise
from a too general view of our working domain. To give a concrete example,
it happens that this theorem has a simple proof for the case of polygons,
which are a class of simple curves that occurs very often in most important
problems. Therefore, proving the theorem for this particular case (a much
simpler task than proving it for the case of general simple closed curves)
may be of great use in solving a lot of other important problems.
|
|
|
|
| This approach suggests the following idea: choose any fixed direction in the plane. Lead a half-line in that direction, starting at any point p in the same plane with our polygon P. Then this ray will intersect the edges of the polygon an even number of times if p is outside the polygon or an odd number of times if p is inside. | |
| The order of a point q with respect to a polygon P (not
passing through q) is defined as the number of revolutions made
by an arrow joining q to a point p on P, as p
is moved once around along the boundary of P. Then if q has
an even order with respect to P, it is outside and if its
order is an odd number, it is inside P. |
|
Proof of the Jordan Curve Theorem Note: we borrow the terminology and explain the
proof that appeared in "What is Mathematics"[1].
Proof steps:
The proof begins with chosing a fixed direction in the plane. Let this
direction be non-parallel to any of the edges of P. This
can always be done since P has a finite number of edges. We define the concept of parity in the following way: two points
have the same parity if they belong to the same set, either A or
B.
This implies that if any point p1 of A is joined
to any point p2 of B by a polygonal
path, then this path must intersect P because otherwise,
all the points on this path (and p1 and p2
in particular) would have the same parity.
We can now conclude that A is the outside region of P
and B, the inside of P. It follows that for any simple
polygon, no matter its shape, we can say if a point is inside or
outside the poylgon. Just draw a ray from this point and count the
intersections with the polygon. An odd number of intersections means our
tested point was inside and an even number of intersection means
the point was outside the polygon. See
it happening in this Java applet.
|
|
Related Material
|
|
|
|
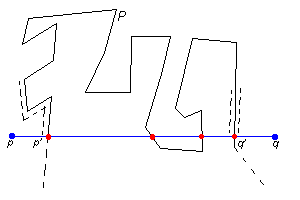 the
segment with P and call that point q'. We now construct a
path starting at p and along the segment pq. Before we reach
p', our path separates from pq and from the boundary of P
but continues along this boundary until it reaches the continuation of
pq. Finally, it comes back to q'. Does this path actually
intersect pq between q' and q? If we can show that
this is the case, then we have the desired path from p to q,
which does not intersect P. This path will be obtained by continuing
the original path along q'q until q is reached. Let's stop
for a moment and note that any two points r and s close enough,
but on opposite sides of an edge of P, always have different parity.
This is true since the ray from one point (say r) will intersect
P in one more point than the ray from the other point (say q).
Back to our case, the parity changes as our path crosses pq between
q' and q, since p, q and all other points on
this path have the same parity. Therefore we have an intersection
point between q' and q, so we can obtain a path between p
and q, which does not intersect P. Since p and q
belong to the same set (from our original supposition), the theorem for
the case of polygons is now proved.
the
segment with P and call that point q'. We now construct a
path starting at p and along the segment pq. Before we reach
p', our path separates from pq and from the boundary of P
but continues along this boundary until it reaches the continuation of
pq. Finally, it comes back to q'. Does this path actually
intersect pq between q' and q? If we can show that
this is the case, then we have the desired path from p to q,
which does not intersect P. This path will be obtained by continuing
the original path along q'q until q is reached. Let's stop
for a moment and note that any two points r and s close enough,
but on opposite sides of an edge of P, always have different parity.
This is true since the ray from one point (say r) will intersect
P in one more point than the ray from the other point (say q).
Back to our case, the parity changes as our path crosses pq between
q' and q, since p, q and all other points on
this path have the same parity. Therefore we have an intersection
point between q' and q, so we can obtain a path between p
and q, which does not intersect P. Since p and q
belong to the same set (from our original supposition), the theorem for
the case of polygons is now proved.