Proof
Let S be a set of n disjoint segments in the plane and l a given direction.We assume that all motions are translations only in the same direction l and that each segment is moved only once and one-at-a-time.
Without any loss of generality, we can assume that the direction l in which the segments are to be separated is the positive x-direction. By induction, if there exists one segment in S that can be moved horizontally rightward without colliding with any other, the segments are separable along that direction, because after we move that one to infinity, the resulting problem is the same for a subset of S.
Let us illuminate all the segments from x=+ ![]() ,
as shown in the following Figure:
,
as shown in the following Figure:
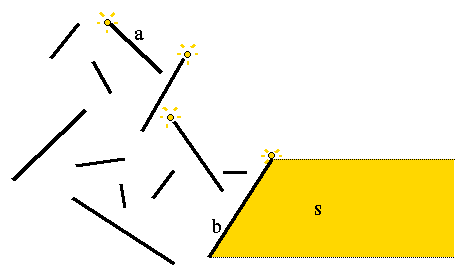
Is there always one segment completely illuminated?
Lemma: In any collection of disjoint line segments,
there is always at least one that is completely illuminated from x=+ ![]() .
.
Proof: Consider the subset U of segments whose upper endpoint is illuminated, that is, a horizontal rightward ray from their upper endpoint does not hit any segment. There is at least one segment in U : the rightmost segment whose upper endpoint is the highest.
As shown in the Figure, this rightmost highest segment
is not necessarily completely illuminated. It can be hidden by a segment
below. However, our claim is that the segment b in U
with the lowest upper end point is completely illuminated. Let
s be the infinite strip to the right
of b. Because the upper endpoint of b is visible
from x=+ ![]() , if any portion
of s is blocked by a segment c, the upper endpoint
of c must lie in s. Then, the highest upper
endpoint of all the segments blocking s must
be illuminated, contradicting our assumption that
b has the lowest illuminated upper endpoint.
, if any portion
of s is blocked by a segment c, the upper endpoint
of c must lie in s. Then, the highest upper
endpoint of all the segments blocking s must
be illuminated, contradicting our assumption that
b has the lowest illuminated upper endpoint.