An O(kn) Time Algorithm for Finding an Ear
A very simple algorithm exists for finding an ear in the simple polygon P :
Function FindEar(P)
1. i = 0
2. ear not found = true
3. while ear not found
4. if
pi is
convex then
5. if triangle formed by
pi-1, pi, and
pi+1
contains no
concave vertex then
6. ear not found =
false
7. if ear not found then
8. i = i + 1
9. return pi
End FindEar
By the Two-Ears Theorem, simple polygon P has at least 2 ears if the number of vertices is > 3. If the number of vertices is 3, then P is a triangle and forms 1 ear. By the definition of a polygon, there is always at least 1 ear in P for the algorithm to find.
To complete the proof of correctness, it suffices to prove the following lemma :
Lemma: If a convex vertex pi is not an ear, then the triangle formed by pi-1, pi, and pi+1 contains a concave vertex.
Proof: If pi is not an ear, then the triangle formed by pi-1, pi, and pi+1 contains a vertex. Let pj be the vertex in the interior of this triangle (pi-1, pi, pi+1) such that the line L through pj and parallel to the line through pi-1 and pi+1 is as close to pi as possible. Let a and b be the points of intersection of line L with the polygon edges (pi, pi+1) and (pi-1, pi) respectively. Triangle (a, pi, b) has no vertices in its interior and lies entirely inside P. Vertices pj-1 and pj+1 must lie on the opposite side of line L, so pj is a concave vertex.
Q.E.D.
The proof of correctness for algorithm FindEar is complete.Q.E.D.
Lines 1 and 2 of FindEar run in constant time. The loop in line 3 is executed at most n - 2 times, which occurs when P has only 2 ears and is similar to this :
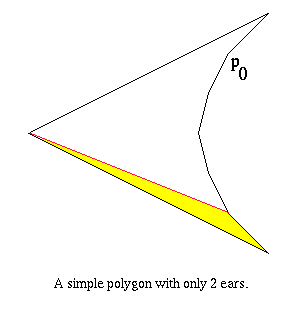
The start vertex for FindEar is p0. If the vertices are sorted in clockwise order, the ear shown in yellow is the first ear found. The number of vertices checked in order to find this ear is n - 2 (where n is the number of vertices in P).
Line 4 runs in constant time. Line 5 may require O(k) time where k - 1 is the number of concave vertices in P since it is possible that all concave vertices are checked for being in triangle (pi-1, pi, pi+1). Lines 6, 7, 8, and 9 all run in constant time.
So, since line 5 may be executed in time proportional to n, algorithm FindEar runs in O(kn) time. However, since k - 1 is the number of concave vertices, the algorithm can be as bad as O(n2).
This page was last updated on Wednesday, December 10th, 1997.
© 1997 Ian Inc.