The One-Mouth Theorem
The One-Mouth Theorem was developed and proven by Godfried T. Toussaint at McGill University in 1991 [7].

Construct the convex hull CH(P) where P is a non-convex simple polygon. Since P is non-convex there must exist edges on the boundary bd(CH(P)) that are not edges of P. Each such edge forms the "lid" of a "pocket" of CH(P). We shall prove that in fact every such pocket yields a mouth. Let Kij denote the pocket of CH(P) determined by vertices pi and pj of P. Kij = {pi, pi+1, ..., pj} U {pj, pi} forms itself a simple polygon. By the Two-Ears Theorem Kij must have two ears and since they are non-overlapping they cannot both occur at pi and pj. Therefore, at least one ear must occur at pk for i < k < j. Obviously such an ear for Kij is a mouth for P.
Q.E.D.
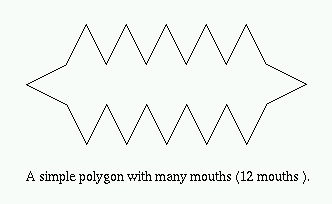
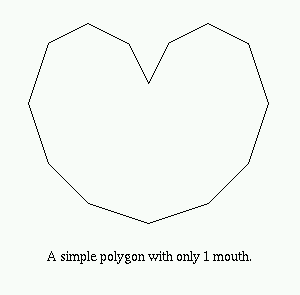

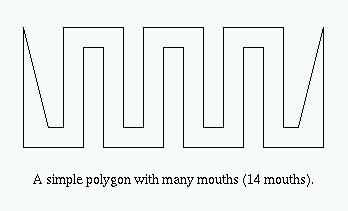
Anthropomorphic polygons are simple polygons that contain precisely two ears and one mouth [7].
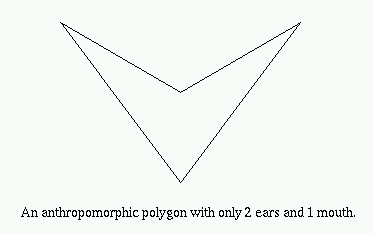
This page was last updated on Wednesday, December 10th, 1997.
© 1997 Ian Inc.