Proof :
Let's first illustrate this lemma with an example :
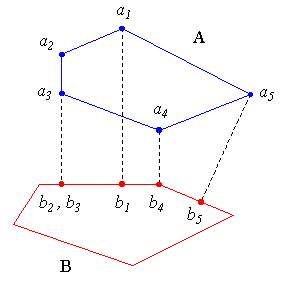
As shown above, moving from b1 to b2 follows a counterclockwise path on the boundary of B, while b3 to b5 implies a clockwise traversal. Because no movement occured from b2 to b3, b3 is called a stationary point.
So, suppose now we go along a chain monotone in some direction d, from a point an to an+1 :

If we put by hypothesis that bn is the closest
point of B from an, where can be located
bn+1 ?
We already proved (lemma 1b) that line L is a
supporting line of polygon B, which is located below L. So
bn+1 can only be below L.
However, bn+1 can not be below L at the right of
P : any point in that area is further from an+1 than
bn. If there is no point of B on the left side of P, then
bn+1 could only be at the same place than
bn. Except for this case,
bn+1 can not be neither on P, because any
point on P below L is also further from
an+1 than
bn.
So bn+1 is necessarily below L, but most
important, at the left of P, that is in the same direction d that we went from
an to an+1. We
conclude that moving along a direction d on a monotone chain of
ai's make bi's move in
the same direction. In the worst case, some bi may
be at the same place than bi-1 (stationary point), but
this doesn't change our conclusion.
Proving lemma 3 is now straightforward :
travelling around a convex polygon
is like moving on two monotone chains of opposite directions. Because
bi's will move in the same direction than
a i's (or maybe not move at all), then the moving
direction of bi's can not change more than twice.
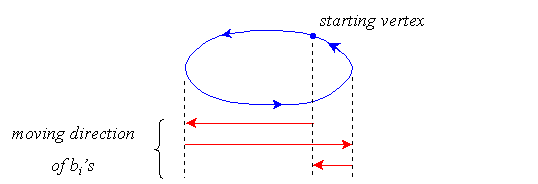
Q.E.D.
Obviously, lemma 3 doesn't say that µ will change twice : for instance, if the starting vertex of the figure above would have been the leftmost or rightmost point of A, then only one change of direction would have had occured. Similarly, we can easily find polygons A and B such that there would be no change in µ, because bi's would move only in one direction, or not move at all.