
|
Everything You Always Wanted to Know About Alpha Shapes But Were Afraid to Ask |

|
by François Bélair |

|
Everything You Always Wanted to Know About Alpha Shapes But Were Afraid to Ask |

|
by François Bélair |
|
|

|

|
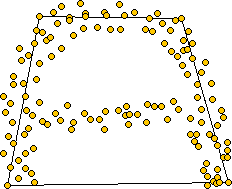
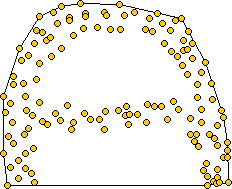
First, let us define a generalized disk of radius 1/alpha to be the following:
Then, given a set of points and a specific value for alpha, we construct the alpha shape graph in the following way:
![]()