Characterizing and Efficiently Computing
Quadrangulations of Planar Point Sets
Algorithm
Existence
of Quadrangulation
We may wonder about the existence of quadrangulations.
In the paper presented here, the following theorem is presented:
Theorem: A set
of points S in general position admits a quadrangulation if and only
if the convex hull of S has an even number of points.
The first part of this theorem is proved by
induction, by constructing a valid quadrangulation from a point on the
convex hull. The second part is proved by a simple counting argument.
Sequential
Insertion Algorithm
The preceding proof implies the following
simple algorithm for quadrangulating a set of points (shown in pseudo-code
here):
-
Step 1: Compute the convex hull in
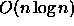 .
.
-
Step 2: Partition the convex hull in
O(n) time by joining one vertex to every other vertex of
the polygon in a clockwise fashion.
-
Step 3: Insert the remaining points
one at a time, forming quadrilaterals as you go.
The algorithm is depicted in figure 1.
The crucial part of this algorithm is step
3. Insertion of the points has to be done efficiently, and it turns out
that it can be performed in 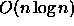 by a simple sweep-line algorithm. So the complexity of this algorithm is
by a simple sweep-line algorithm. So the complexity of this algorithm is 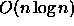 .
.
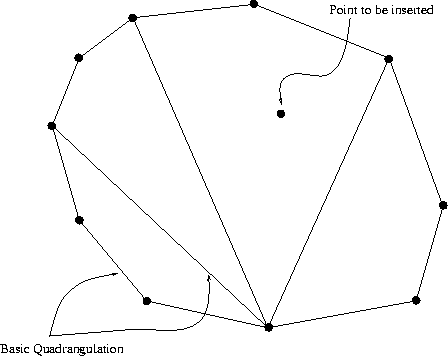
Figure 1: Sequential Insertion
Algorithm
Although this algorithm is optimal from
a theoretical point-of-view, it has several drawbacks:
-
Modification of the sweep-line algorithm to
insert the points in the quadrangulation is non-trivial.
-
It leads to poor quadrangulations, with
thin/long quadrilaterals.
Spiraling
Rotating Calipers Algorithm
The alternate approach presented here is to
show that a set of points S always admits a simple spanning polygonal
chain that in turn admits a hamiltonian triangulation. Then, by removing
every other diagonal starting at one end of the chain, we will obtain the
desired quadrangulation except perhaps a single triangle at the end. In
this case, we will add a single Steiner point there to complete the quadrangulation.
-
Computing
the convex spiral of the set of points
-
Triangulating
the spiral
-
Quadrangulating
the spiral's path
-
Algorithm
summary
-
Theorem
-
Experimental
results
Computing
the convex spiral of the set of points
We begin by computing the polygonal chain.
The polygonal chain used is the convex spiral of S (an example of
a convex spiral is depicted in figure 2) . It is easily computed in 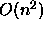 by using a Jarvis march, in the following way:
by using a Jarvis march, in the following way:
-
Step 1: start with the current point
as the min-x point
-
Step 2: search for the first point
encountered clockwise, among the unmarked points,
-
Step 3: mark this point and put it
in the polygonal chain
-
Step 4: move the current point to this
point
-
Step 5: go back to step 1, until no
more points are unmarked
Unfortunately, this simple algorithm ruins
the desired complexity ( 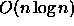 ). However, this structure is closely related to the convex layers
of a set (or onion peeling of a set), and one can compute the convex
spiral from the convex layers, one from the other, in O(n)
time. One can also compute the convex layers of a set in
). However, this structure is closely related to the convex layers
of a set (or onion peeling of a set), and one can compute the convex
spiral from the convex layers, one from the other, in O(n)
time. One can also compute the convex layers of a set in 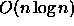 time using the algorithm of Chazelle or Hershberger/Suri. So this convex
spiral can be computed in
time using the algorithm of Chazelle or Hershberger/Suri. So this convex
spiral can be computed in 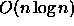 time.
time.
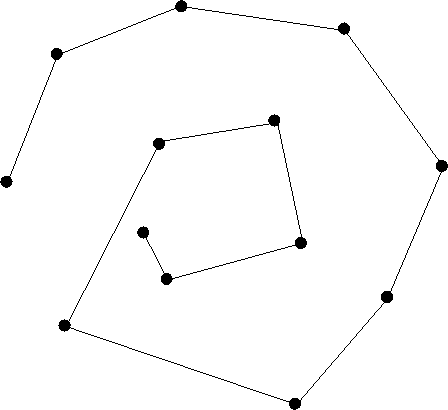
Figure 2: A convex spiral of a
set of points
Triangulating
the spiral
Once we have the spiral, we need to triangulate
it. For this, we will first split the chain into two parts: and inner star-shaped
polygon and an outer polygonal chain.
We extend the last inner segment of the
polygonal chain to make this separation (see figure 3). The inner part
is star-shaped and can be triangulated trivially.
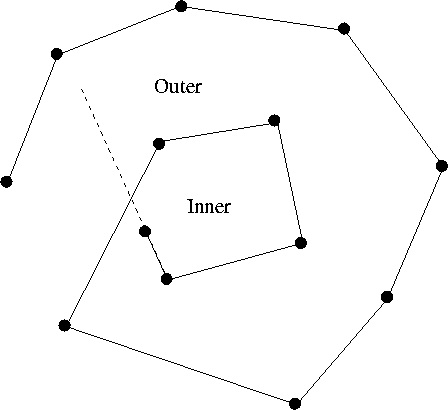
Figure 3:
Inner and outer chains.
Triangulating the outer part of the chain
is accomplished by using a variant of the rotating calipers algorithm.
This method consists of using two lines to follow the outer chain's vertices
in an order that will lead to a triangulation. It is quite simple:
-
Step 1: start with the two closing
vertices
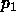 and
and 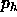 , and two tangent lines vertical.
, and two tangent lines vertical.
-
Step 2: Rotate the two lines clockwise
until one of them touches the next vertex of the chain it is currently
on
-
Step 3:
Add a diagonal between the two points and move the point that touched the
chain in step 2 to the next vertex on its chain
-
Step 4: If the chain is not completely
triangulated (i.e. the two vertices aren't
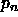 and Y), loop to step 1
and Y), loop to step 1
An example of the rotating calipers is depicted
in figure 4.
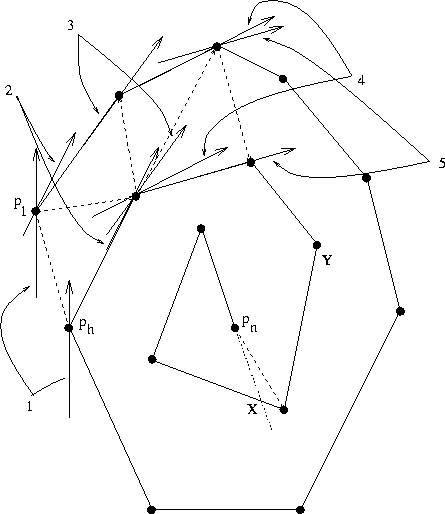
Figure 4: The rotating calipers
in action.
From these steps, we obtain a triangulation
of the spiral (which has for dual an Hamiltonian path).
Quadrangulating
the spiral's path
To obtain a valid quadrangulation, we need
only start at the center of the spiral, and delete every other diagonal
as we proceed towards the exterior.
When we get at the exterior end of the
spiral (at 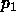 and
and 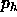 ), we might have a triangle there. All we need to do is add a Steiner point
there (i.e. an extra point) to close it with a valid quadrilateral.
), we might have a triangle there. All we need to do is add a Steiner point
there (i.e. an extra point) to close it with a valid quadrilateral.
Algorithm
summary
Here is a description of the algorithm, as
was implemented in the accompanying Java Applet. You can examine this algorithm
by running the applet, which lets you see these steps one at a time:
-
Step 1: Validate the input vertices
for general position. We simply discard any coincident vertices. The applet
does not check for collinearity yet.
-
Step 2: Compute a spiral polygonal
chain by using the rotating calipers method (the convex spiral of
the set S). This is actually implemented in
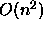 but can theoretically be done in
but can theoretically be done in 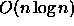 .
.
-
Step 3: Close the polygonal chain at
the starting end
 ,
,  .
.
-
Step 4: Split the spiral into inner/outer
regions by extending the line through
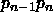 . The inner region is star-shaped, and therefore we triangulate it easily.
. The inner region is star-shaped, and therefore we triangulate it easily.
-
Step 5: Triangulate the outer region
of the spiral, starting at the inner end.
-
Step 6: Remove one out of 2 diagonals
of the whole spiral triangulation, starting at the center. This way we
obtain quadrilaterals.
-
Step 7: Optionally add a Steiner point
to complete the last polygon of the chain, which may otherwise be a triangle.
-
Step 8: Show the complete quadrangulation.
Theorem
From the preceding SRC algorithm, the following
theorem follows:
Theorem: Let S
be a set of n points in general position in the plane. Then S may be quadrangulated
with the addition of at most one Steiner point in 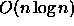 time.
time.
The Steiner point for the quadrangulation
is only necessary if the number of vertices on the convex hull of S
is odd.
This algorithm generalizes to k-quadrangulations:
all we need to do is to remove more than one diagonal in the removal phase.
Then, to complete the last polygon, we need only add at most k-3
Steiner points!
Corollary: A k-angulation
of a set of points can be achieved with the addition of at most k-3 extra
points.
Main Page
| Abstract
| Introduction
| Algorithm
| Results
| Applet
| References
| Comments
![]() by a simple sweep-line algorithm. So the complexity of this algorithm is
by a simple sweep-line algorithm. So the complexity of this algorithm is ![]() .
.




![]() and
and ![]() ), we might have a triangle there. All we need to do is add a Steiner point
there (i.e. an extra point) to close it with a valid quadrilateral.
), we might have a triangle there. All we need to do is add a Steiner point
there (i.e. an extra point) to close it with a valid quadrilateral.
![]() time.
time.