La Géométrie taxi???

La géométrie Euclidienne définit la distance entre deux points A et B  grâce à la formule suivante (qui vient du théorème de Pythagore):

d(A,B) = sqrt ((xA-xB)2 + (yA-yB)2 )
Il s'agit certainement de la notion la plus intuitive de distance, mais elle n'est pas la seule définition raisonnable. La théorie des espaces métriques étudie justement les propriétés et les analogies qui existent entre diverses définitions de la distance entre deux éléments d'un ensemble. Par exemple, on peut très bien décider de définir la distance entre A et B par:
 d(A,B) = |xA-xB| +  |yA-yB|

En termes plus concrets, la distance entre deux points devient dans ce cas la somme des distances horizontale et verticale entre A et B. Cette définition est relativement naturelle: il s'agit de la distance qu'aurait à parcourir un taxi qui voudrait se rendre du point A au point B dans une ville ou toutes les rues sont orientées soit horizontalement, soit verticalement. C'est pour cette raison que l'on appelle cette distance la distance taxi ou la distance Manhattan.

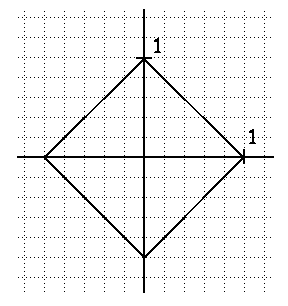
Plusieurs figures géométriques, tels les cercles, les paraboles, les hyperboles, sont définies en termes de distance. Ainsi, un cercle se définit comme l'ensemble des points dont la distance au centre est égale au rayon. Bien sûr, en modifiant la définition de distance, la forme de ces figures changent de façon importante. L'exemple du cercle en géométrie taxi est sans doute le plus célèbre.
 

 
 Cercle taxi

On obtient un carré!  (Bien entendu, ceci ne résoud pas le célèbre problème de la  quadrature du cercle!) En effet, tous les points de ce carré sont de coordonées (x,y) telles que |x| + |y| = 1.
De façon plus générale, les côniques (comme les cercle, hyperboles, paraboles) vont devenir plus "carrées" en géométrie taxi. Voici deux exemples tirés de la page web de Julie VanBelkum. 



Hyperbole taxi



parabole taxi

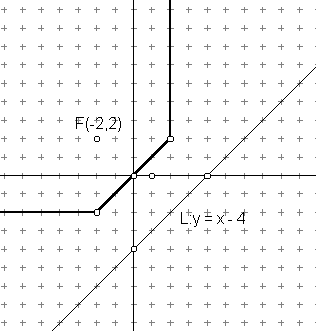
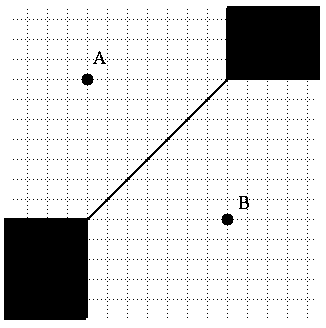
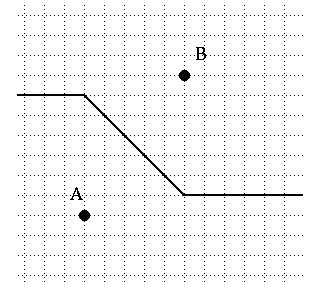
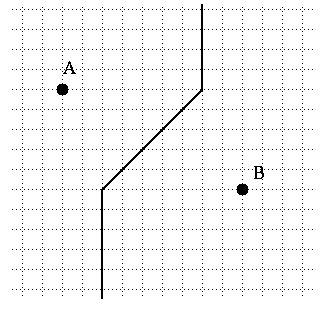
Une autre figure importante dont la définition repose sur la distance est celle de l'ensemble des points situés à égale distance de deux points donnés A et B. En géométrie Euclidienne, cet ensemble est simplement la médiatrice du segment [AB]. Les choses se compliquent par contre lorsque l'on adopte la distance taxi. On peut distinguer quatre exemples de base:
 
 
Cas 1: |xA-xB|  < |yA-yB| 
Cas 2: xA = xB
Cas 3: |xA-xB|  > |yA-yB| 
Cas 4: |xA-xB|  = |yA-yB| 
Ces exemples ne sont pas trop complexes. Notons que lorsque  xA = xB, les médiatrices euclidienne et "taxi" coincident. Dans les cas 1 and 3,  la médiatrice taxi est composée de segments soit verticaux, soit horizontaux à l'extérieur du rectangle défini par A et B et d'un segment de pente 1 ou -1 à l'intérieur. Dans le dernier cas, nous obtenons une étrange figure car tous les points des coins inférieur droit et supérieur gauche sont en fait équidistants de A et B en géométrie taxi.
 
De retour à la page titre