Comparative Musicology - Musical Rhythm
and
Mathematics
- some of my work -
"There can be no music without rhythm." - Igor Stravinski
"The mathematics of rhythm are universal. They don't belong
to
any particular culture." - John McLaughlin


Comparative Musicology - Musical Rhythm
and
Mathematics
- some of my work -
"There can be no music without rhythm." - Igor Stravinski
"The mathematics of rhythm are universal. They don't belong
to
any particular culture." - John McLaughlin

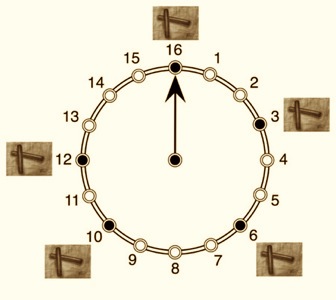
In July of 2003 I co-organized the First International Workshop on Computational Music Theory. A few days into the workshop I proposed that we should analyse the Flamenco meters (compas) from the mathematical point of view. During the workshop we discussed the topic and agreed to search the literature. After the workshop I came up with what I thought would be an appropriate measure of meter similarity that I called the directed swap distance. This distance considers the rhythm as a binary string, and a swap is a position interchange of an adjacent '1' and '0' (note and silence). Later I learned that a continuous linear-assignment with cost equal to the distance between assigned elements, used in Computational Biology, is equivalent to the swap distance. Together with my student Justin Colannino, we published an efficient algorithm for calculating it (see reference below). The phylogenetic analysis of the Flamenco meters with this measure yielded very interesting results, and we decided to publish them. The preliminary results were presented at the BRIDGES conference in 2004. An extended version in Spanish was subsequently published in the La Gaceta.
The publication of our article in La Gaceta has generated a lot of media interest in Spain and Canada. Spanish musicologists and flamenco historians pretty well agree that the Fandango is the fountain (and oldest) of all Spanish dances, and that the cradle or birthplace of the Fandango is the city of Huelva in Andalucia (in southern Spain). The phylogenetic analysis we performed confirmed these tenets.Flamenco and Mathematics links:
- Flamenco and Mathematics (Google)
- matematicas y flamenco.
- Museo de Arte Famenco, "El Flamenco y las Matematicas," Monday, September 12, 2005.
- Alicia R. Mediavilla, "Flamenco y Matematicas," Al Fondo, 2005.
- English version translated by Yasha Maccanico, "Flamenco and Maths".
- Also appears in: Nataraja.
- Francisco Dancausa Ruiz, "El Flamenco Visto por las Matematicas," August 8, 2005.
- CanalSocial Noticias, Un estudio revela la relacion matematica entre los principales estilos del flamenco, August 11, 2005.
- Spanish newspaper: El Pais - September 7, 2005.
- "Las Matematicas Con el Flamenco," Genciencia, Tuesday, January 24, 2006.
- "Matematicas y Flamenco," Solo Ciencia.
- La Voz de Galicia, "FLAMENCO Y MATEMATICAS", April 28, 2006.
Other media:
